久々の新変光星の発見とVSX登録
このところずっと、ぎょしゃ座のある星を観測していたら、10日ほど前にその写野で暗い星が変光していることに気が付きました。今までの観測フレームを見直したら何度もその星が写っているので測光してデータを処理したらほぼ0.80日の周期のEAとわかりました。明るいときで17等でUCAC4カタログには記載はありません。ASAS-SNデータをダウンロードして周期をさらに細かく決めることが出来たのでVSXに登録申請しましたが、セバスチャンがZTFのデータをダウンロードしてもっと良い周期が得られるはずだと忠告してくれたので、初めてZTFデータを使ってみました。そうしたら見事な位相図が得られました!ZTFがこの変光星を発見していなかったのがちょっと不思議です。

おそらく私が今まで発見した変光星の中でで一番暗いでしょう。
Gaia DR2のGmag、BPmag、RPmagデータから B - V 、V - Rc、 V - Ic などの色指数の推定値を得る
7月20日のブログでB - V と BP - RPという色指数の関係式について書きました。
Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(4) - muttenz's blog
ここにB - V 、V - Rc、 V - Ic とBP - RP の関係図と推定式をまとめておきます。
B - V

g(B - V) = -0.083509 * bprp ^ 3 + +0.282372 * bprp ^ 2 + +0.580821 * bprp + -0.014337
Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.083509 0.002595 -32.180 < 2e-16 ***
b 0.282372 0.009104 31.016 < 2e-16 ***
c 0.580821 0.010190 56.999 < 2e-16 ***
d -0.014337 0.004268 -3.359 0.000787 ***
V - Rc

g(V - Rc) = -0.0204691 * bprp ^ 3 + +0.0967384 * bprp ^ 2 + +0.3545388 * bprp + +0.0145966
Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.0204691 0.0006667 -30.70 <2e-16 ***
b 0.0967384 0.0023388 41.36 <2e-16 ***
c 0.3545388 0.0026178 135.43 <2e-16 ***
d 0.0145966 0.0010965 13.31 <2e-16 ***
V - Ic

g(V - Ic) = 0.0071876 * bprp ^ 3 + +0.0635081 * bprp ^ 2 + +0.7474902 * bprp + +0.0573296
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 0.0071876 0.0009006 7.981 1.72e-15 ***
b 0.0635081 0.0031593 20.102 < 2e-16 ***
c 0.7474902 0.0035362 211.384 < 2e-16 ***
d 0.0573296 0.0014811 38.707 < 2e-16 ***
最後になりますが、Gaia DR2の各バンドの特性のグラフです。(Gaia DR2のサイトから取りました。)緑がGバンド、青がBP

Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(6)
最後にIcバンドに関する図、推定式です。




Ic= Gmag - ( 0.003467 * bprp ^ 3 + -0.090290 * bprp ^ 2 + 0.718688 * bprp + 0.038816)
gIcとLandoltからのIcの差の標準偏差は
Ic= 0.0214
Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(5)
今までBバンドとVバンドの推定式を記載しましたが、同様にRcバンドについて図と推定式を記載します。



推算式です。
Rc= Gmag - (-0.024190 * bprp ^ 3 + -0.057060 * bprp ^ 2 + 0.325737 * bprp + -0.003917)
gRc - Rc の標準偏差は 0.0214 です。
Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(4)
今までの続きとして、RcバンドとIcバンドに関して記述してもよいのですが、別の視点からデータを解析してみました。
先日大島修さんが掲載しておられた「測光システムとフィルター 標準星」
を読んだ時のことを思い出しました。
今までは Gmag - V(Landolt) を左辺に、右辺に BPmag - RPmagの3次式を置き、3次式の係数を求めていました。左辺で2つの測光システムが混ざっています。
なんとなくスッキリせず、左辺をB - V (BもVもLandoltから)としたらどうだろうかと考えました。
つまり、Landoltからの B - V をy軸に、Gaia DR2からの BP-RP をx軸にプロットし3次式のモデル式の係数を求めました。

B-Vという色指数とBP-RPという色指数の関係となり、かなり直線に近く右上がりで、ほぼ(0,0)の原点を通ります。
GaiaデータのbprpのみからB-Vを推定できます。
g(B - V) = -0.083509* bprp ^ 3 + 0.282372 * bprp ^ 2 + 0.580821 * bprp + -0.014337
パラメータです。
Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.083509 0.002595 -32.180 < 2e-16 ***
b 0.282372 0.009104 31.016 < 2e-16 ***
c 0.580821 0.010190 56.999 < 2e-16 ***
d -0.014337 0.004268 -3.359 0.000787 ***
ところでgBを求める式は
gB = Gmag - ( 0.079788 * bprp ^ 3 + -0.436169 * bprp ^ 2 + -0.609623 * bprp + -0.004176)
でした。
gVを求める式は
gV = Gmag - (-0.003721 * bprp ^ 3 + -0.153798 * bprp ^ 2 + -0.028802 * bprp + -0.018513)
でした。上の式から下の式を左辺、右辺それぞれ引くとGmagは消えて
gB - gV = - ( 0.079788 * bprp ^ 3 + -0.436169 * bprp ^ 2 + -0.609623 * bprp + -0.004176) + (-0.003721 * bprp ^ 3 + -0.153798 * bprp ^ 2 + -0.028802 * bprp + -0.018513)
式をまとめるとbprp ^ 3、bprp ^ 2、bprp、定数それぞれの係数は
- 0.079788 -0.003721 = -0.083509
0.436169 + -0.153798 = 0.282371
0.609623 + -0.028802 = 0.580821
0.004176 + -0.018513 = -0.014337
となり、B - Vとbprpの関係式を直接求めた式の係数が出ました。(上記のパラメータ参照)
つまり
g(B - V) = gB - gV
でした。
一つの同じデータから二種類のプロセスで得た結果ですから同じ係数が出ても不思議はないのですが、ここまで合うとは思いませんでした。
Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(3)
Vバンドに関して行ったことをBバンドでもやりました。
説明は同じなので省いて、図だけを掲載します。




Gaia DR2から推定したBバンドの光度gBの推定式は
gB = Gmag - ( 0.079788 * bprp ^ 3 + -0.436169 * bprp ^ 2 + -0.609623 * bprp + -0.004176)
となります。
標準偏差は0.0539 でVの場合よりやや悪いです。
パラメータです。
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 0.079788 0.002650 30.104 <2e-16 ***
b -0.436169 0.009298 -46.909 <2e-16 ***
c -0.609623 0.010407 -58.576 <2e-16 ***
d -0.004176 0.004359 -0.958 0.338
Gaia DR2のGmag、BPmag、RPmagデータからVmagなどの推定値を得る 新しい試み(2)
Landoltの星表にある各星の位置情報からそれに対応するGaia DR2のデータを取得することを金田さんがやってくださったわけですが、プログラムでそれを自動化してもそう簡単なことではなかったそうです。
Landoltに記載の星でGaia DR2に対応する星がなかったり、2つの星が出てきたりとか、Gaia DR2のデータの一部が欠けていたり、bprpの値が適用範囲外だったりで、16等未満の星の中から326件を除外しなければならなかったそうです。そうやってLandoltとGaia DR2のデータとを対応できたのが前回書いた6070個の星を含む星表となりました。
必要なデータが出揃ったので、B、V、Rc、Ic各光度ごとに前回記述したようにプロットして非線形回帰のモデル式
y = a x (bprp) ^ 3 + b x (bprp) ^ 2 + c x (bprp) + d
の三次式の係数をR言語の nls 関数で求めました。
ここではVの場合を説明します。
ある星のGmagとLandoltからのVmagの差をy軸に、BPmagとRPmagの差をx軸にとってLandoltの星表の星をプロットします。その図で黒点一つ一つが星表の星を表しています。

nls 関数を用いて算出した各係数は図中のとおりです。
Gaiaから推算したgV光度とすると、上の式を変形して、
gV = Gmag - ( a x (bprp) ^ 3 + b x (bprp) ^ 2 + c x (bprp) + d )
によってGmag、BPmag、RPmag から各星のgV推定光度を算出します。
下はそのgVを縦軸に、LandoltからのVを横軸に採ったグラフです。

この図からわかるようにgVとLandoltからのVmagはかなりよくあっています。そこで、その差をとって、それがVmagによってどのように分布するかを次の図にしました。

当然予想されることですが、星が暗くなるとgVとVmagの差が大きくなっていきます。
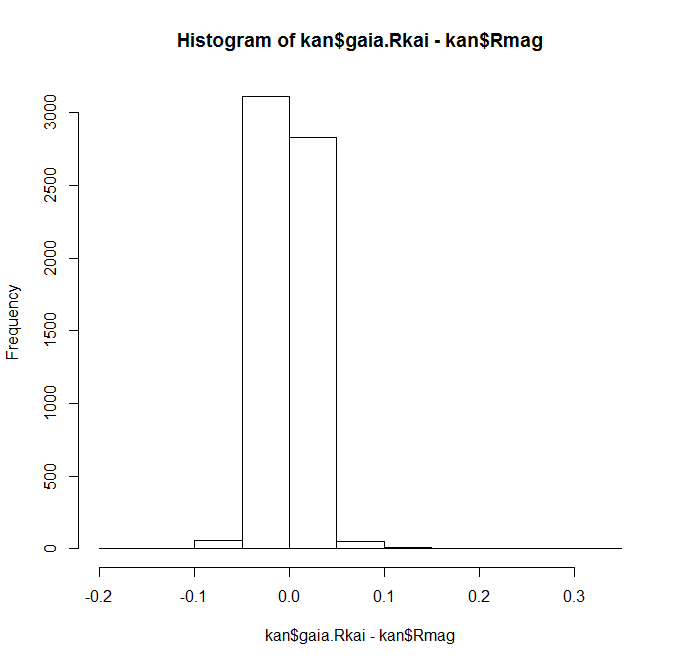
かなり外れているものも見受けられるのですが、6000個に比べたら比較的少ないとも考えられます。このヒストグラムを作ってみました。

このように大部分の星でそのGaiaからの推定値はLandoltの値から0.05等以内に入っています。
実際に標準偏差は0.0199等でした。
gVの推算式を書いておきます。
gV = Gmag - (-0.003721 * bprp ^ 3 + -0.153798 * bprp ^ 2 + -0.028802 * bprp + -0.018513)
なお、nls関数で求めた係数に関するパラメータを下に書いておきます。
Parameters:
Estimate Std. Error t value Pr(>|t|)
a -0.0037209 0.0009801 -3.796 0.000148 ***
b -0.1537979 0.0034385 -44.729 < 2e-16 ***
c -0.0288018 0.0038486 -7.484 8.26e-14 ***
d -0.0185133 0.0016120 -11.485 < 2e-16 ***