EASolverを少し改良

先日ブログに書いたEASolverを少し改良してみました。

devianceはいわばO-Cの自乗和なのですが、仮定している周期が長ければO-Cが当然大きい値になり得るし、仮定している周期を短くすれば小さくなるわけです。

極端な話、周期を0.001日位に仮定したら自乗和もほぼそれ以下になるわけですから、仮定している周期の自乗とO-Cの自乗和との比(P^2)/devを取って、その大小で周期を評価したほうが良いかと考えました。（大きいほど確からしい）

実際のスクリプトは下の方に書いておきます。（極小のデータの数、ｍが大きいと当然devも増えるわけで、(m*P^2)/devでそれぞれの周期を評価するのがもっと良いかもしれません。）

このように改良したスクリプトで、CW Oriのホフマイスターのデータを使って実際にやってみました。（この星の周期の改訂を2014年にVSXに届けました。）

これがホフマイスターの極小観測データです。

2425202.61 13.5
2425245.49 13.5
2425298.47 13.5
2425322.33 13.5
2425346.35 13.5
2425676.33 13.5

改良したスクリプトで周期を1－20日の範囲で探させました。

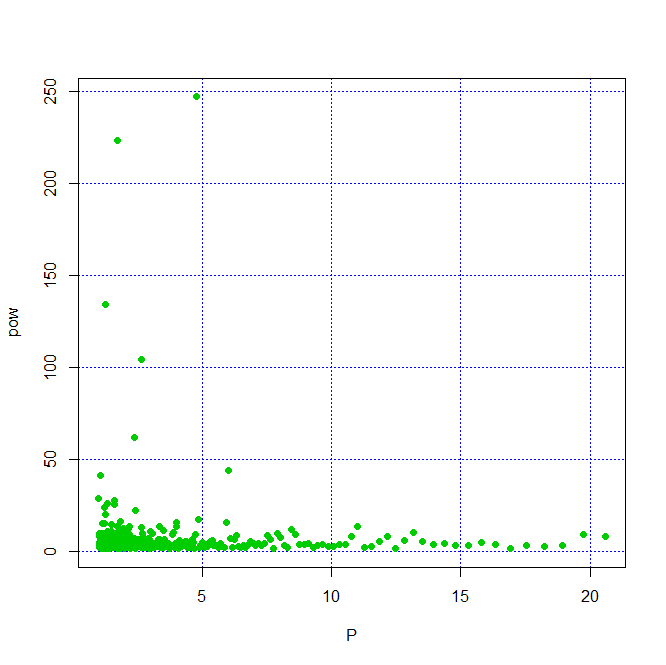
ベスト３の周期です。

ホフマイスターが出した周期は4.78505で、今でもGCVSにそう記載されており、彼がこの周期を正しいと思ったのも当然のようです。

私が観測データやASASデータなどから得た実際の周期は1.70993でした。

一発で正解、とはいかないようですが、このように候補をかなり絞れそうです。

下のグラフは改良前のスクリプトで作ったものです。1日－5日の範囲で探させました。

下はペランソのEASolverで延々と時間をかけて探させた場合です。

改良前のスクリプトの結果によく似ています。

３つの候補は出てきますが、順位が全く逆です。

改良したスクリプトです。ところどころ前のスクリプトと違う文字を使用していますので、全部載せます。

# mini: vector with m elements of minima(HJD) in ascending order
# Period to search between P1: minimum period & P2: maximum period

P1 <- 1
P2 <- 20
options(digits=12)
m <- length(mini)
d <- mini - mini[1]
d[m] # distance between the first & the last minimum in day

N1 <- floor(d[m] / P2)
N2 <- ceiling(d[m] / P1)
n <- N2 - N1
pow <- vector("numeric",n+1)

for (i in 1:(n+1)) {
P <- d[m] / (N1 + i - 1)
N <- round(d / P)
res <- lm(d ~ N)
dev <- deviance(res)
pow[i] <- (P^2) / dev
}

plot(d[m]/(N1+(1:(n+1))-1),pow, pch=16,col=3,grid(col=4),xlab="P")

max(pow)
N0 <- N1 + which.max(pow) - 1
N0 # N for the last minimum
P0 <- d[m] / N0
P0 # found Period
N <- round(d /P0)
res <- lm(mini ~ N)
coef(res) # improved epoch & Period
residuals(res) # residuals for each minimum

ord <- order(pow, decreasing=T)
P <- d[m] / (N1 + ord[1:3] -1)
P # the best 3 periods